Global positioning system (GPS) is a satellite based navigation system that provides the user with accurate position and time information. Today we find GPS receivers in almost every field – right from car navigations systems to missile launches, mobiles to aircraft - GPS is becoming an integral part of our lives. Here is an attempt to make the readers better understand the GPS system and to some extent, the techniques involved in its working
GPS consists of a constellation of satellites (at least 24) that are deployed into orbits of 20000km. The data transmitted by the satellites is a Direct sequence spread spectrum (DSSS) signal with each satellite having a unique PRN (pseudo random noise) code of its own. The satellites are identified by this unique code that is a part of the signal that they transmit. The satellites have Ids from 1 to 32.
The orbits are inclined at an angle of 55 degrees to the equatorial plane. The choice of orbit is such that there are at-least 5 satellites visible to a GPS receiver (with an open sky view) from any point on earth. The satellites orbit the earth with an orbital period of 12hrs. Hence the visibility scenario at any point on earth repeats itself every 24 hrs. It simply means that, if at a particular point on earth, I see satellites with Ids 2, 4, 10, 17, 25, and 20 then I would see the same set of satellites tomorrow at the same time.
The basic idea of GPS positioning – Trilateration
Trilateration is the basic theory behind GPS positioning. Let me explain this in very simple terms.Consider a planar (2D) system in which I have three reference points or base stations (BS) which are transmitting signals and a mobile station (MS) or a receiver capable of receiving and decoding the signal from these base stations. The positions of these BS are fixed and are known to the MS.
Let us assume that the data sent by each of the BS has sufficient information such that the MS is able to calculate the accurate range or distance from the BS i.e. if MS decodes signal from BS1, it can obtain its exact distance from BS1.
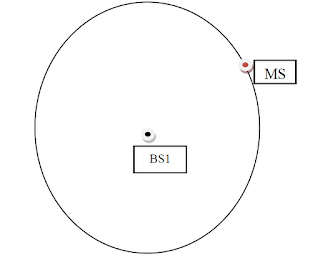
Now, I know my distance (d1) from BS1 and as said earlier, I know the location of BS1. This means that the position of the MS is anywhere on the circle centered at BS1 and with a radius d1.
Similarly if the MS can decode the signal from BS2 and obtain the distance d2 from it, then the ambiguity associated with the position of MS reduces to the intersection of the two circles (with BS1 and BS2 as centers and d1 and d2 as radius respectively). Hence the position is either point A or point B as shown in the figure. Extending this idea to one more BS reduces the ambiguity to a point that is the intersection of all the three circles thus formed.
Now that you are convinced with the position determination in 2D space, we can extend the same to position determination in 3D space with MS being your GPS receiver and BS being the satellites in orbit. The range information from one satellite would give you a sphere, two satellites would give you a circle and three satellites would give you two points. One of these points, the true position will be towards the surface of the earth and the other will be on the other side of the satellite orbit and is discarded.
NOTE:
GPS consists of a constellation of satellites (at least 24) that are deployed into orbits of 20000km. The data transmitted by the satellites is a Direct sequence spread spectrum (DSSS) signal with each satellite having a unique PRN (pseudo random noise) code of its own. The satellites are identified by this unique code that is a part of the signal that they transmit. The satellites have Ids from 1 to 32.
The orbits are inclined at an angle of 55 degrees to the equatorial plane. The choice of orbit is such that there are at-least 5 satellites visible to a GPS receiver (with an open sky view) from any point on earth. The satellites orbit the earth with an orbital period of 12hrs. Hence the visibility scenario at any point on earth repeats itself every 24 hrs. It simply means that, if at a particular point on earth, I see satellites with Ids 2, 4, 10, 17, 25, and 20 then I would see the same set of satellites tomorrow at the same time.
The basic idea of GPS positioning – Trilateration
Trilateration is the basic theory behind GPS positioning. Let me explain this in very simple terms.Consider a planar (2D) system in which I have three reference points or base stations (BS) which are transmitting signals and a mobile station (MS) or a receiver capable of receiving and decoding the signal from these base stations. The positions of these BS are fixed and are known to the MS.
Let us assume that the data sent by each of the BS has sufficient information such that the MS is able to calculate the accurate range or distance from the BS i.e. if MS decodes signal from BS1, it can obtain its exact distance from BS1.
Now, I know my distance (d1) from BS1 and as said earlier, I know the location of BS1. This means that the position of the MS is anywhere on the circle centered at BS1 and with a radius d1.
Similarly if the MS can decode the signal from BS2 and obtain the distance d2 from it, then the ambiguity associated with the position of MS reduces to the intersection of the two circles (with BS1 and BS2 as centers and d1 and d2 as radius respectively). Hence the position is either point A or point B as shown in the figure. Extending this idea to one more BS reduces the ambiguity to a point that is the intersection of all the three circles thus formed.
Now that you are convinced with the position determination in 2D space, we can extend the same to position determination in 3D space with MS being your GPS receiver and BS being the satellites in orbit. The range information from one satellite would give you a sphere, two satellites would give you a circle and three satellites would give you two points. One of these points, the true position will be towards the surface of the earth and the other will be on the other side of the satellite orbit and is discarded.
NOTE:
- Even though it seems that only three satellites are essential for position determination, in practice 4 are required due to the low precision clock on the receiver (more about this later)
- The positioning can also be thought of as a linear system of three unknowns (position co-ordinates x, y, and z) of the receiver, which requires at-least three equations to solve. These three equations are obtained by three satellites.
- The fourth unknown called the user clock bias requires the range information from the fourth satellite.


This is true for a geographical position in two dimensions.In order to calculate the value of height spanning up the 3rd dimension a fourth satellite is need - creating 4 spheres rather than circles intersecting in 1 point. nice write up
ReplyDelete